Modern memory systems are much more complicated than the traditionally assumed virtual and physical address space separation. We explain in this post which effects can not solely expressed by the basic model and are important for correct function of operating systems. We summarize our recent paper. In this work we present a theory for addressing in such modern memory subsystems. We formalize the theory in Isabelle/HOL.
Today’s operating system, text books and also verification efforts assume a quite simple memory model: Applications execute in a virtual address space, virtual addresses get translated into the physical address space by a MMU. In this physical address space the systems DRAM and memory mapped registers of devices are located. If there are devices that perform direct memory accesses (DMA), they access the physical address space directly. This model is depicted in Figure 1.
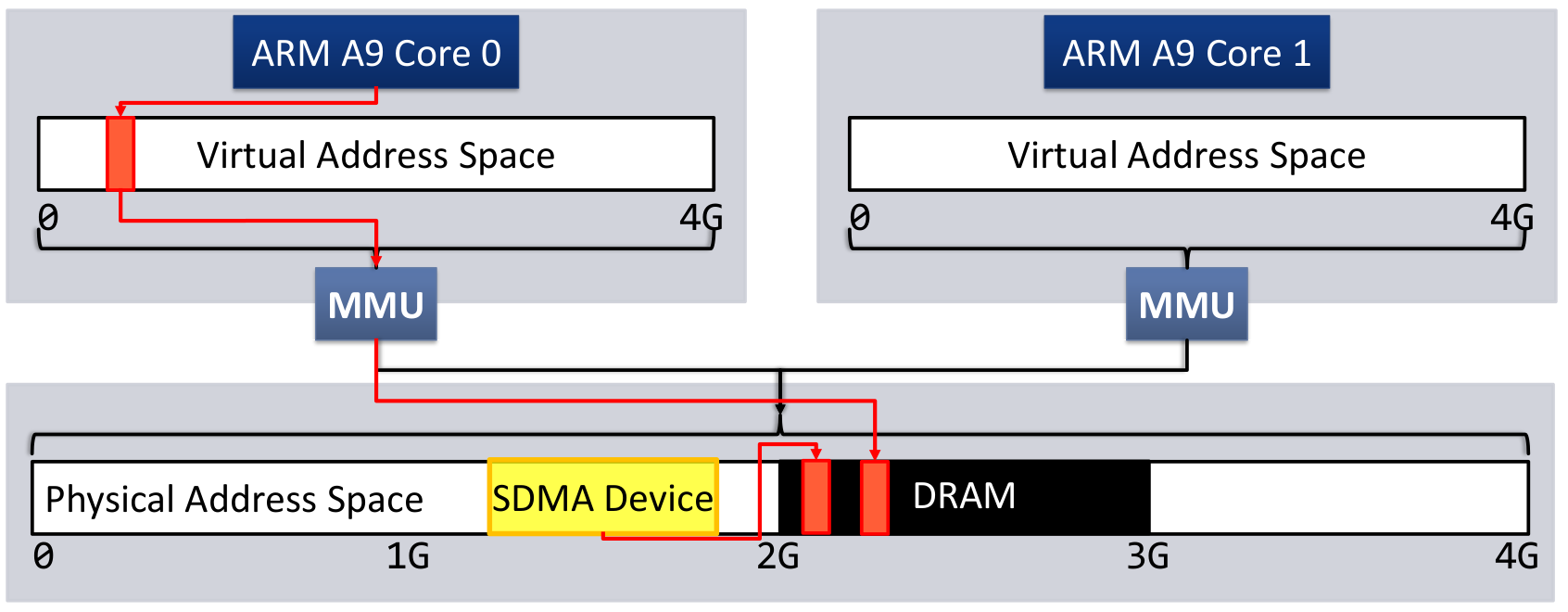Fig1. The traditional view of memory systems
However, on real systems this simplistic view fails to capture the necessary details for correct operation. In a previous workshop paper we have discussed a variety of real systems and shown that more complicated systems are indeed common. Let me show you one example to illustrate some effects we encounter in Fig2.
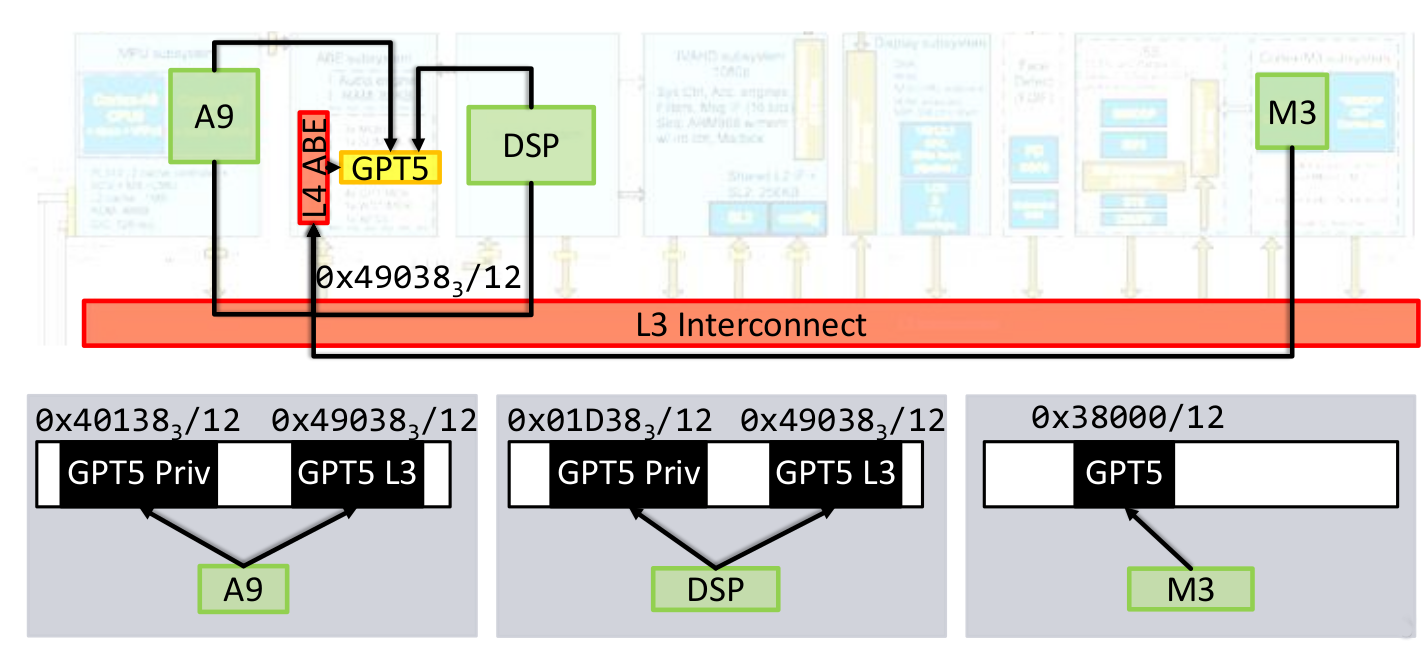Fig2. A real system (excerpt)
This figure shows how different cores can access the GPT5, a memory mapped
general purpose timer. The physical address that a core has to issue depends
on the core, the A9 core has two option of reaching the device, either using
the private interface to the timer using the base address 0x40138000 or accessing
the timer through the L3 bus using the address 0x49038000. Address synonyms
(two addresses that access the same physical
location) are not expressible in the simplistic memory model.
Accessing the same location from the DSP is possible, but a different address
has to be used. The M3 core has to issue again a different address, even though
the memory accesses passes through the same interconnect. In such a system
it does not make sense anymore to talk about a physical address space, every
actor has its own view of the system. These effects are quite common, for
instance on x86 platforms each CPU has its own local APIC registers,
that all appear under the same address.
Since the simplistic model is not powerful enough, we need something better. We noted there is no physical address space anymore, hence the notion of a physical or absolute address does not make sense anymore. Instead we focus on talking about relative addresses. We call a relative address plus the node on which this address is to be interpreted as name. The nodes in our system have two properties: They can accept addresses, and they can translate addresses. To model caches which either accept or translate, depending on the cache state, we permit addresses that translate to multiple output addresses. Our system of nodes forms a directed graph.
A natural question to ask is, where does a certain name end up when issued on this node. A difficulty in this is that our system permits loops. A real system that has memory addressing loops is probably faulty or misconfigured, but we do not want to rule this out in our modeling approach. In fact, showing the absence of such misconfiguration in any real system is one of our future tasks. In the paper we give a set theoretic and an operational definition of the resolve function. We show that they are equivalent, under the assumption that the operational resolution actually terminates. Because of this assumption, we study under which conditions termination actually occurs. The rank function assigns each name a natural number and it must decrease every time a translate step is taken. We found that specifying a rank function is a necessary and sufficient condition for termination.
While the decoding net captures the essential details, it is not a very handy representation for use in an operating system. If we fix one observer, we can derive a simplified decoding net that resembles the two layer simplistic model. We do so by collapsing all the translate steps into one. We formalized this process and show that it preserves view-equivalency for the chosen observer. View equivalent means that the same address resolves to the same address.
In a real operating system, we implement a data structure that refines the decoding net. However, we also must populate this datastructure. How this is done depends on the system we are running on. Certain platforms offer discovery mechanisms, such as ACPI. On other platforms, this information can not be discovered and must be provided by the operating system developer. In this case, we need to be able to express a decoding net in some form of syntax. The syntax presented in the paper adds two syntactical extensions to the plain decoding net that are focused on expressing real systems: First, the syntax works with ranges of addresses, because often whole address blocks are remapped. Second, the introduction of an overlay concept. If a node overlays another, it will map all addresses not otherwise mapped to that node. We show that the syntax refines the decoding net.
Based on this syntax we have developed a system description language that we use as a runtime representation of the memory system and at compile time to generate initial kernel page tables.
A further application is expressing real hardware with respect to the decoding net. To showcase this, we model a simple software loaded translation lookaside buffer (TLB) in Isabelle and map each of its configuration state to a model node.
